기하: 두 선분의 교점
DESCRIPTION
(x1, y1)과 (x2, y2)을 지나는 직선 1과 (x3, y3)과 (x4, y4)를 지나는 직선 2가 있을때, 서로 다른 두 직선의 교점은 다음 선형 방정식을 통해서 계산 할 수 있다.
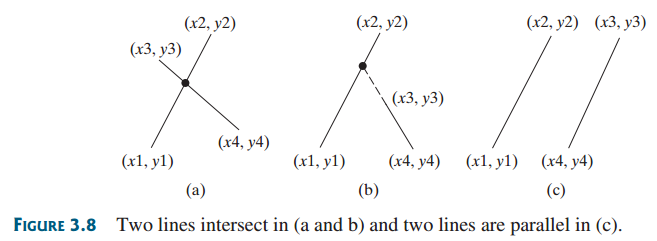
Two points on line 1 are given as (x1, y1) and (x2, y2) and on line 2 as (x3, y3) and (x4, y4), as shown in Figure 3.8a–b. The intersecting point of the two lines can be found by solving the following linear equation:
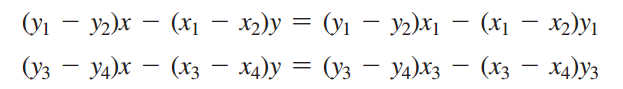
위 선형 방정식의 해는 “4326 - 대수: 2 * 2 선형 방정식 풀이” 문제에서 사용한 Cramer’s rule 을 통해 계산 할 수 있다. 만약 선형 방정식의 해가 존재하지 않는다면 두 직선은 평행한 것이다. 당신은 2개의 직선을 나타내는 4개의 점을 입력받아 두 직선의 교점을 출력하는 프로그램을 작성하려고 한다.
This linear equation can be solved using Cramer’s rule (see Programming Exercise 3.3). If the equation has no solutions, the two lines are parallel. Write a program that prompts the user to enter four points and displays the intersecting point.
INPUT
-
Line 1 : 첫번째 선의 좌표 x1 y1 x2 y2 (각각 실수이며 공백으로 구분됨)
-
Line 2 : 두번째 선의 좌표 x3 y3 x4 y4 (각각 실수이며 공백으로 구분됨)
두 직선은 서로 다른 직선이다.
OUTPUT
- Line 1 : x y 값을 출력 (소수점 첫째자리에서 버림, 예: 11.263의 경우 11.2로 출력하고 11.0의 경우 11.0로 출력, -11.256의 경우 -11.2로 출력 두 직선이 만나지 않을 경우 parallel출력)
SAMPLE INPUT
2 2 7 6
4 2 -1 -2
SAMPLE OUTPUT
parallel
HINT
소수점 한자리까지 출력 System.out.printf(“%.1f\n”, 0.6789);
Comments